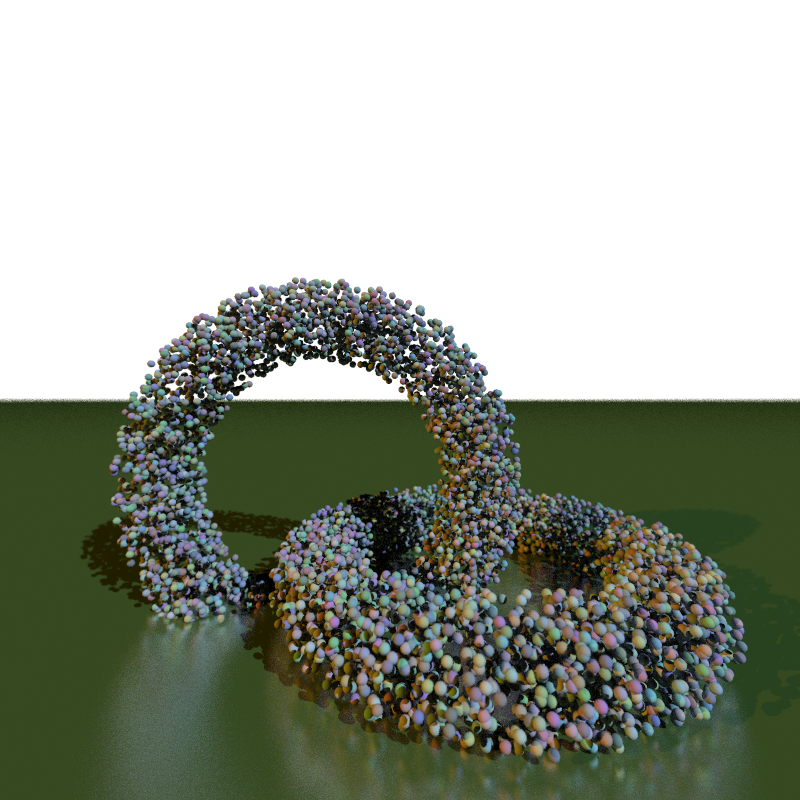This programming assignment creates 3D imagery using ray tracing. In most other respects, its logistics are similar to the rasterizer assignment: you code in any language you want and your program reads a text file and produces an image file.

1 Core

Implement a raytracer with spheres, diffuse lighting, and shadows. In particular, this means

1. Write a program that reads a .txt file and produces a .png file. It will be invoked as e.g. ./yourprogram exampleInput.txt, via a makefile.

2. Handle the input file keywords png, color, sphere, and one sun, with proper handling of sRGB gamma.

3. Implement the ray-sphere intersection algorithm. These algorithms are defined down to the pixel in almost all contexts, and should match the provided input files and their outputs very closely. Almost all successful submissions follow our ray-sphere intersection pseduocode closely.

4. Implement shadows with shadow rays, including preventing shadow acne.

2 Electives

You may stop after implementing the core parts. Elective parts may be implemented in any set of MPs, and getting 0 electives here is fine if you do extra electives elsewhere.

3 What you submit

For this MP you submit one program, in any language of your choosing, that implements all of the core and any elective functionality you choose. The program will be executed as follows:

make build
make run file=rast-grey.txt
make run file=rast-smallgap.txt
# ...
make run file=rast-points2.txt

See the associated warm-up for more on how to set up a Makefile and generate PNG images.

It is tedious to grade output files for inputs you haven’t implemented. Because of that you’ll be asked to submit a file named implemented.txt which lists the optional parts you implemented; in particular, it should be a subset of the following

exposure  
suns      
camera          
lenses          
plane      
triangle   
barycentric
map        
bulb       
reflect         
refract         
rough           
antialias   
focus           
global          
BVH             

Submitting a file that says you implemented something you didn’t may result in a small professionalism penalty for wasting grader time.

4 Test Files

All test input files, reference output files, and supporting files can be downloaded as a zip

4.1 Core

Input	Output	Notes
ray-sphere.txt		Because there is no sun, nothing is lit. If you see the central sphere but not the one in the corner, the most common reason is failing to normalize ray directions when they are first created.
ray-sun.txt		Numbers generated for pixel (55, 45) Ray origin: (0, 0, 0) Ray direction: (0.0990148, -0.0990148, -0.990148) Intersection depth: 0.724832 Intersection point: (0.0717691, -0.0717691, -0.717691) Surface normal: (0.23923, -0.23923, 0.94103) Sun direction: (0.57735, 0.57735, 0.57735) Lambert dot product: 0.543304 Linear color: (0.543304, 0.543304, 0.543304) sRGB color: (194, 194, 194) Numbers generated for pixel (82, 70) Ray origin: (0, 0, 0) Ray direction: (0.481108, -0.451039, -0.751731) Intersection depth: 1.20665 Intersection point: (0.58053, -0.544246, -0.907077) Surface normal: (-0.838941, 0.511507, 0.185845) Sun direction: (0.57735, 0.57735, 0.57735) Lambert dot product: -0.0817462 Linear color: (0, 0, 0) sRGB color: (0, 0, 0)
ray-color.txt		This file is useful for debugging but is not awarded points and not generated from your code by the submission server.
ray-overlap.txt
ray-behind.txt		There’s another sphere behind the camera that should not be visible.
ray-shadow-basic.txt

4.2 Elective

Input	Output	Notes
ray-expose1.txt		low exposure; note the lit colors for some pixels exceed 1 before exposure but are darkened by exposure to a distinguishable range
ray-expose2.txt		high exposure
ray-suns.txt		several colored suns
ray-shadow-suns.txt		multiple suns means multiple shadows
ray-view.txt		moved and rotated camera
ray-fisheye.txt
ray-panorama.txt
ray-plane.txt		two intersecting planes
ray-shadow-plane.txt		multiple planes and spheres intersecting with shadows
ray-tri.txt		tests that triangle boundaries line up with vertex locations
ray-shadow-triangle.txt		triangles casting and receiving shadows
ray-tex.txt		spheres with textures; uses earth.png and moon.png as texture maps
ray-trit.txt		triangles with textures; uses earth.png and moon.png as texture maps
ray-bulb.txt		two bulbs, one sun; if your image is darker than this one, make sure negative dot products during lighting are clamped to 0
ray-shadow-bulb.txt		spheres with a light between them should not shadow one another
ray-neglight.txt		one of the lights has negative color, emitting darkness; impossible in the real world but not in a computer
ray-shine1.txt		colorless reflectivity
ray-shine3.txt		colored reflectivity
ray-bounces.txt		custom levels of recursion
ray-trans1.txt		colorless transparency
ray-trans3.txt		colored transparency
ray-ior.txt		different indices of refraction on each sphere
ray-rough.txt		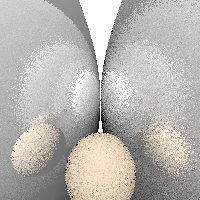different roughness with both reflections and diffuse light; based on random sampling so each run will be slightly different
ray-aa.txt		anti-aliasing; based on random sampling so each run will be slightly different
ray-dof.txt		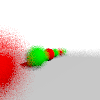depth-of-field effects; based on random sampling so each run will be slightly different
ray-gi.txt		global illumination; based on random sampling so each run will be slightly different
ray-many.txt		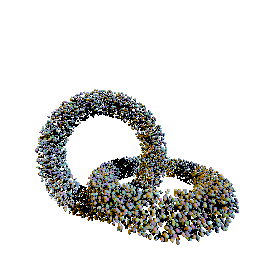10,000 spheres; will be run single-threaded only; a simple BVH adds between a 10× and 50× speedup to this scene

5 Specification and implemention guide

5.1 Ray Emission

Rays will be generated from a point to pass through a grid in the scene. This corresponds to flat projection, the same kind that frustum matrices achieve. Given an image w pixels wide and h pixels high, pixel (x, y)’s ray will be based the following scalars:

s_x = {{2 x - w} \over {\max(w, h)}}

s_y = {{h - 2 y} \over {\max(w, h)}}

These formulas ensure that s_x and s_y correspond to where on the screen the pixel is: s_x is negative on the left, positive on the right; s_y is negative on the bottom, positive on the top. To turn these into rays we need some additional vectors:

\mathbf{e}

the eye location; initially (0, 0, 0). A point, and thus not normalized.

\vec f

the forward direction; initially (0, 0, -1). A vector, but not normalized: longer forward vectors make for a narrow field of view.

\vec r

the right direction; initially (1, 0, 0). A normalized vector, always perpendicular to \vec f.

\vec u

the up direction; initially (0, 1, 0). A normalized vector, always perpendicular to both \vec r and \vec f.

The ray for a given (s_x, s_y) has origin \mathbf{e} and direction \vec f + s_x \vec r + s_y \vec u.

5.2 Ray Collision

Each ray will might collide with many objects. Each collision can be characterized as o + t \vec{d} for the ray’s origin point o and direction vector \vec{d} and a numeric distance t. Use the closest collision in front of the eye (that is, the collision with the smallest positive t).

Raytracing requires every ray be checked against the full scene of objects. As such your code will proceed in two stages: stage 1 reads the input file and sets up a data structure storing all objects; stage 2 loops over all rays and intersects each with objects in the scene. Unlike the rasterizer, there is no explicit draw instruction: all scene geometry in the input file is drawn after you read the whole file.

Many of the elective parts of this assignment have rays spawn new rays upon collision. As such, most successful implementations have a function that, given a ray, returns which object it hit (if any) and where that hit occurred (the t value may be enough, but barycentric cordinates may also be useful); that ray-collision function is called from a separate function that handles lighting, shadows, and so on.

5.3 Illumination

Basic illumination uses Lambert’s law: Sum (object color) times (light color) times (normal dot direction to light) over all lights to find the color of the pixel.

Make all objects two-sided. That is, if the normal points away from the ray (i.e. if \vec d \cdot \vec n > 0), invert the normal before doing lighting.

Illumination will be in linear space, not sRGB, and in 0–1 space, not 0–255. If a color would be brighter than 1 or dimmer than 0, clamp it to the 0–1 range. You’ll need to convert RGB (but not alpha) to sRGB yourself prior to saving the image, using the official sRGB gamma function: L_{\text{sRGB}} = \begin{cases} 12.92 L_{\text{linear}} &\text{if }L_{\text{linear}} \le 0.0031308 \\ 1.055{L_{\text{linear}}}^{1/2.4}-0.055 &\text{if }L_{\text{linear}} > 0.0031308 \end{cases} If you implement anti-aliasing, reflections, transparency, or other techniques that blend multiple colors, make sure you don’t convert to sRGB until after all the colors are combined.

5.4 State machine

To help the files not get messy when many different properties are specified, many options operate on a notional state machine.

For example, when you open the file the current color is white (1,1,1). Any sphere or triangle you see will be given the current color as its color. When you see a color command you’ll change the current color. Thus in this file

png 20 30 demo.png
sphere 0 0 0 0.1
color 1 0 0
sphere 0.5 0 0 0.2
sphere 0.3 0 0 0.3
color 0 1 0

the first sphere is white, the second and third spheres are red and the last color doesn’t do anything.

6 Input keywords

The file may have three types of keywords:

1. the required png keyword will always be first
2. mode-setting keywords are optional, but if present will precede any data or drawing keywords
3. state-setting keywords provide information for later geometry
4. geometry keywords add objects to the scene, using both their parameters and the current state

No drawing happens until after the entire file is read.

6.1 PNG

png width height filename

• always present in the input before any other keywords
• width and height are positive integers
• filename always ends .png
• exactly the same as in the Rasterizer MP

6.2 Mode setting

bounces d

• limits the depth of the secondary ray generation to d
• primary rays have depth 0; secondary rays generated from a ray of depth x have depth x+1; if the depth of a ray would be larger than d, don’t generate that ray
• defaults to 4 if not provided

forward f_x f_y f_z

• sets the forward vector for primary ray generation
• do not normalize; if this vector is longer it will automatically result in a zoomed-in display
• fix the right and up vectors to be perpendicular to forward, as \vec r = \text{normalized}\big(\vec f \times \text{up}\big) and \vec u = \text{normalized}\big(\vec r \times \vec f\big)

up u_x u_y u_z

• sets the target up vector, subject to being perpendicular to the forward vector
• see forward for how the real up vector is computed

eye e_x e_y e_z

• sets the ray origin for primary rays

expose v

• sets the exposure function to use in converting light to screen color
• apply exposure after all other computation and combination of colors, but before sRGB
• if present, use the function \ell_{\text{exposed}} = 1 - e^{-v\ell_{\text{linear}}}
• if absent, us the function \ell_{\text{exposed}} = \ell_{\text{linear}}

Fancier exposure functions used in industry graphics, such as FiLMiC’s popular Log V2, are based on large look-up tables instead of simple math but are conceptually similar to this function.

dof focus lens

• apply depth-of-field using a lens of radius lens and a focual depth of focus
• this is done by randomly perturbing each primary ray’s origin and direction
• new origin should be a random location on a disk with radius lens and center eye which is perpendicular to the forward vector \vec f
• new direction should be picked such that \mathbf{o}_\text{old} + t \vec d_\text{old} = \mathbf{o}_\text{new} + t \vec d_\text{new} where t is the focal depth

aa n

• shoot n rays per pixel and average them to create the pixel color
• when averaging pixel colors, remember that those that hit nothing contribute to alpha but not to RGB; otherwise antialiased boundaries will look darker than they should

panorama

• find the ray of each pixel differently; in particular, treat the x and y coordinates as latitude and longitude, scaled so all latitudes and longitudes are represented
  • keep forward in the center of the screen and up on the top of the screen
  • will never be combined with dof or fisheye

fisheye

• find the ray of each pixel differently; in particular, render the forward hemisphere as an ellipse that fits the image with x and y coordinates proportional to the sine of the angle
  • keep forward in the center of the screen and up on the top of the screen
  • if s_x^2 + s_y^2 > 1, don’t shoot any rays
  • the easiest way to achieve this is to use \sqrt{1-s_x^2-s_y^2}\vec f instead of just plain \vec f in the ray direction computation
  • will never be combined with dof, panorama, or non-unit-length forward

gi d

• render the scene with global illumination with depth d
• when lighting any point, include as an additional light the illuminated color of a random ray shot from that point
• secondary rays can shoot more secondary rays, with a maximum depth d; this is tracked separatel from, but similarly to, the reflection/refection depth from the bounces keyword
• distribute the random rays to reflect Lambert’s law by picking the ray direction to pass through a randomly selected point inside a sphere that is tangent to the surface at the ray’s origin

6.3 State setting

color r g b

• sets the current RGB color
• given in RGB color space where 0 is black, 1 is white
• do not clamp these values; negative and more-than-1 values are permitted
• use the unclamped floating-point color values as is until the very end; the order is
  1. all computation, including any antialiasing
  2. exposure, if that mode is enabled
  3. linear to sRGB, clamping to the 0–1 range
  4. sRGB to bytes
• defaults to (1,1,1) if not provided

texcoord u v

• sets a texture coordinate for subsequent xyz keywords
• defaults to (0,0) if not provided

texture filename.png

• sets the texture map for subsequent tri and sphere keywords
• for triangles, the texture coordinates are given by texcoord
• for spheres, the texture coordinates are the latitude and longitude of the intersection point
• texture none disables textures, reverting to color
• defaults to none if not provided

roughness \sigma

• sets the standard deviation of surface normals for subsequent tri and sphere keywords
• if \sigma > 0, randomly perturb the surface normal by a delta in x, y, and z each taken from a Gaussian distribution with mean 0 and standard deviation \sigma, then re-normalize, prior to performing illumination, refraction, or reflection
• defaults to 0 if not provided

shininess s_r s_g s_b

• sets the ratio of light that is reflected instead of being diffused, absorbed, or refracted

• if given with just one parameter, like shininess 0.4, use it for all three color channels

• from page 153 of the glsl spec, the reflected ray’s direction is \vec{I} - 2(\vec{N} \cdot \vec{I})\vec{N} where \vec{I} is the incident vector, \vec{N} the unit-length surface normal

• reflected rays that hit nothing should be treated as opaque black

• when combining transparency and shininess, shininess takes precedent

  the input snippet

  shininess 0.6
  transparency 0.2

  combines to make an object 0.6 shiny, (1 − 0.6) × 0.2 = 0.08 transparent, and (1 − 0.6) × (1 − 0.2) = 0.32 diffuse

• see bounces for preventing infinite recursion when two shiny objects reflect one another

• defaults to 0 if not provided

transparency t_r t_g t_b

• sets the ratio of light that is refracted instead of being diffused or absorbed

• if given with just one parameter, like transparency 0.4, use it for all three color channels

• from page 153 of the glsl spec, the refracted ray’s direction is computed as k = 1.0 - \eta^2 \big(1.0 - (\vec{N} \cdot \vec{I})^2\big) \text{ray direction} = \eta \vec{I} - \big(\eta (\vec{N} \cdot \vec{I}) + \sqrt{k}\big)\vec{N} where \vec{I} is the incident vector, \vec{N} the unit-length surface normal, and \eta is the index of refraction; if k is less than 0 then we have total internal reflection: use the reflection ray described in shininess instead

• refracted rays that hit nothing should be treated as opaque black

• see ior for the index of refraction to use

• see bounces for preventing infinite recursion when two shiny objects reflect one another

• defaults to 0

  Transparency has many pieces that all have to be correct to result in a good image: two intersections (entering and exiting) with different angles, indices of refraction, and normals, with nontrivial mixed vector and trigonometric computations. Transpadenct is the portion of this MP that most often goes wrong when first attempted, and is difficult to debug because each error causes its own kind of inaccurate image, but those images are not easily distinguished.

ior \eta

• sets the index of refraction for transparent materials
• defaults to 1.458 if not provided

6.4 Geometry

sphere x y z r

• add a sphere with center (x,y,z) and radius r to the list of objects to be rendered
• capture any current state as part of the sphere’s material

sun x y z

• add an infinitely-far-away light source coming from direction (x,y,z)
• capture the current color as the light’s color

bulb x y z

• add a located-in-the-scene light source coming from location (x,y,z)
• capture the current color as the light’s color
• the light source is a mathematical point, and hence too small for any primary ray to see
• in-the-scene light decreases with the square of distance, \frac{1}{d^2}
• recall that objects behind light sources don’t cast shadows, only objects in front of them

plane A B C D

• add an infinite plane satisfying the equation Ax+By+Cz+D=0
• (A,B,C) is the normal of the plane
• the point \dfrac{-D(A,B,C)}{A^2+B^2+C^2} is on the plane
• it is common to see incorrect shadows where the plane vanishes in the distance; this is not a concern for this class

xyz x y z

• defines a vertex location for future tri commands
• captures the current texcoord
• does not capture other data: color, texture, roughness, etc are handled by tri, not xyz
• store this in a list separate from other geometry; it will be index by later tri

tri i_1 i_2 i_3

• defines a triangle connecting three vertice from previous xyz commands
• indices are 1-based; negative indices count from the back of the current vertex list
• capture any current state as part of the triangle’s material

7 Just for fun

We have a few larger scenes you can try if you want something a bit more challenging: